Netf�ix a�d Ch�ll?
Note: No prior knowledge of Golang or online dating required for this post
You’re having so much fun exploring the ins and outs of the Go programming language that you decide its time to finally start working on that social network dating app for meeting surfer chicks you’ve always wanted to build. While you’re super excited about the seemingly endless list of features you have planned, you’re quickly growing tired of meeting girls on Tinder just to find out that they boogie board. A decision is made to focus on the most important feature and ship an alpha version two weeks from today. The target audience is young, single millennials - a generation completely comfortable with experiencing the world through a 2.5x4.5 inch digital screen. Although our parents had to pick up the phone and call a potential date, we’re cool with sending a quick text and ending it with that cute cactus emoji. Because who doesn’t like that thing?
🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵🌵
Emojis are dope and even though technology continues to completely change the dating experience, its clear communication is still key. You start with feature number 1 - messaging. Messaging has two requirements:
- Messages have to be 10 characters or less
- Messages MUST support emojis
V1 ships and everything’s going great. Your inbox is flooded with messages from
all types of surfer girls, and you’ve spent the last few days really hitting it
off with Lauren from Brooklyn. She’s smart, funny, and well travelled - a point
made very clear by the Chinese symbol on her forearm from Spring Break 2012 her
trip through Southern China . Hey, even though it might not even actually mean
wave, it beats the pura vida tattoo Jackie picked up on her two-day layover in
Costa Rica. You wait 19.5 minutes, because you obviously can’t risk seeming too
eager, and reply with an idea you had for your own Chinese symbol tattoo.
characters: 11/10
message: “cool 海洋?”
Wait. What? As much as you try to type “cool 海洋?”, the app says you’re over the character limit. Something’s wrong. There’s only 8 characters with the space, clearly under the 10 character limit, yet the app is saying there’s 11 and you can’t click send.
Go is an awesome language, but there are for sure a few gotchas for new Gophers. Let’s take a look at the code that validates a given message is under the character limit.
const charLimit = 10
func isUnderMsgLimit(msg string) bool {
return len(msg) <= charLimit
}
A constant, charLimit, is initialized with a value of 10. A function,
isUnderLimit, is declared which takes 1 string argument, msg, and returns a
boolean - true if the length of msg is less than or equal to charLimit, and
false otherwise.
You scratch your head, and conclude the language is wrong and can’t do basic arithmetic - Thanks Rob Pike. Until you finally do the reasonable thing and look up the documentation for the builtin package’s len function.
Aha! When len is passed a string it returns the number of bytes in the string
and NOT the number of characters - a little different than some other languages
you might have experience with, like Ruby’s definition of length defined on the
String class.

So why does this happen? Its actually pretty simple. In Go, all strings are just slices of bytes. So when you take the length of “海洋” its actually taking the length of the slice containing the bytes representing those characters. We can convert the string to its byte slice representation with T(v), which converts the value of v to type T.
[]byte(“海洋”)
=> [230, 181, 183, 230, 180, 139]
len([230, 181, 183, 230, 180, 139])
=> 6
len("海洋")
=> 6
These are the same thing, just one, the byte array, is mutable, while the string is not (strings in Go are immutable). But this leads us to the next question. Why do some strings seem to have one byte per character while others use more?
len("foo")
=> 3
[]byte("foo")
=> [102, 111, 111]
len("海洋")
=> 6
[]byte("海洋")
=> [230, 181, 183, 230, 180, 139]
To answer this we’re going to have to take a bit of a detour and learn what a character really is to a computer.
Character Encoding
Let’s count from 0 - 9.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Okay, great! Now how about 0 - 10?
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Wait! What did you just do there? I understand that 1 comes after 0 and 3 comes after 2. I even remember learning why 6 is afraid of 7, but how did you get from 9 to 10? You probably didn’t even think twice about what came after 9. Obviously its 10. And what about 99? What comes next? 100! And after 100? 101!
Do you remember all those hours spent learning to count? To tell you the truth my memory is pretty fuzzy about those early years, but how about learning your times tables? I clearly remember the flashcards, worksheets, and quizzes we spent an entire year going over in the 1st grade. We take it for granted now, but your teachers, family, and friends put a considerable amount of effort into teaching you one of the most widely used counting systems in the world - the decimal system.
But, before we go there let’s back up a bit and quickly go over how we got to where we are today.

Unary
It all started with the number 1. Well, not actually the number 1, but the idea of one being a single unit of something. 1 could be represented with a single tick:
I
One more than one could be represented with two ticks.
II
Two more than one could be represented with three ticks.
III
To keep this short, let’s just say that in unary the amount n can be represented with n ticks. Here’s twenty represented in unary:
IIIIIIIIIIIIIIIIIIII
The Romans

Soon enough the world saw civilizations expanding, mathematics and languages developing, and the Roman Empire hell-bent on world domination. The Romans were pretty smart, and one day a whole bunch of them got together and hashed out a wild idea: “Wouldn’t it be rad if we could turn these ticks into unique symbols that better represent their value”.
One could be represented with:
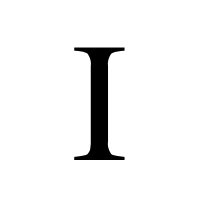
Two could be represented with:

And five could be:

Clearly much easier to work with than their unary alternatives:
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Yes, these symbols look a bit cooler and make for some awesome tattoos, but the real genius is exposed when you understand how the Romans took advantage of position to change the meaning of a given symbol.
These Roman nerds understood that four is really just one less than five and can be represented by placing the I to the left of V:

Six is really just one more than five and can be represented by placing the I to the right of five:

Decimal
Fast forward a couple of years and we find another group of smart peeps thinking about this same concept of a symbol’s position having a huge significance on its value. These smart peeps were the inventors of the decimal system and the rest of this post can be attributed to their findings (as well as this quadruple IPA I happened to have stumbled upon a few hours ago).
Taking influence from the Roman’s numeral system, the decimal system uses something called positional notation, which is simply a way of encoding, or representing, numbers - Positional notation uses the same symbols, also called glyphs, combined with placeholders signifying different orders of magnitude to represent any number value in the world. The order of magnitude applied is also known as a radix - which in the case of the decimal system is 10. For this reason decimal is referred to as base 10 and takes its name from the Latin decimus meaning tenth. Take for example the number 6,523:
6,523

Pictured above is each number with its corresponding order of magnitude based on its position. Reading this right-to-left using positional notation we could say.
There are:
3 ones
2 tens
5 one-hundreds
6 one-thousands
for a total of 6, 523
We can do this for any number in the universe. To represent 23 we use the same notation.
There are:
3 ones
2 tens
for a total of 23
Binary
Alright, so that was a pretty fun trip down memory lane, but you’re probably wondering how the hell this possibly relates to programming? Well computers, it turns out, use a similar counting system. While the decimal system uses ten distinct glyphs to represent every number in the entire world, a very convenient fact for those of us living with ten fingers, what happens when you don’t have the blessing of ten glyphs, or fingers? Is there a way to represent every number in the world with only two symbols, or in our case two signals - off and on? Sounds wild, but there is. Its called binary and everything from your phone, to your MacBook, to your hover board uses this counting system every single day.
Bi comes from Latin binarius, meaning consisting of two. Binary has two glyphs, 0 and 1, and like the decimal system, uses the power of positional notation. In this case its based on multiples of 2, which gives it the name base 2. Let’s follow the same rules we used before and write some binary. Below we have the number 38 represented in binary.
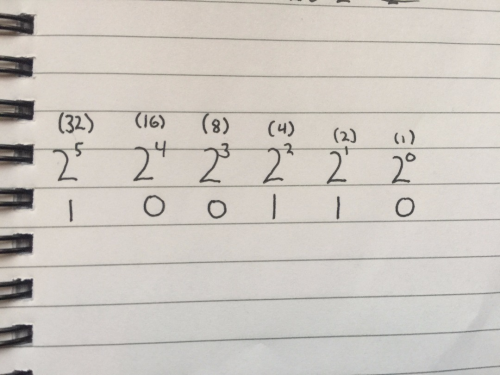
Using positional notation to read right-to-left there are:
0 ones
1 two
1 four
0 eights
0 sixteens
1 thirty-two
for a total 38!
What is the maximum number that can be represented in base 2 with 8 positions?
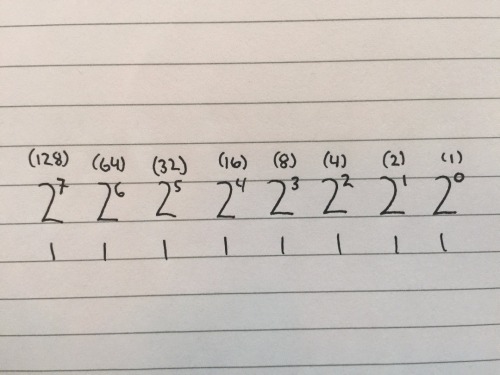
1 one
1 two
1 four
1 eight
1 sixteen
1 thirty-two
1 sixty-four
1 one-hundred-twenty-eight
for a total of 255.
So, with 8 placeholders we can represent 0- 255 or 256 unique values. And if we substitute the word placeholder with bit, then we can say that with 8 bits we can represent 256 different values. Further, understanding that 8 bits combine to make 1 byte, we can conclude that with 1 byte, we can represent 256 values.
note: A bit is the most basic unit of information a computer can store. 0 or 1, off or on. Since bits don’t tell us much on their own, we address them in groups of 8, and call this 1 byte.
So, using a combination of just two signals off or on, a computer is capable of representing any number in the world. While this is awesome, you’re still probably wondering how this relates to our initial problem of potentially losing a date because our application thinks that our message is too long. Let’s take a very brief look at our last counting system before moving onto how this translates to computers representing characters.
Hexadecimal
It turns out that after a while developers got really tired of constantly writing 1 and 0 to describe their programs’ memory usage, and set out to think of a more concise way to describe the values these 0s and 1s represent. Some smart, fed-up, 0-and-1-hating-programmer came along and decided that instead of using base 2 or base 10, what if they used a radix of 16, also known as hexadecimal? The Greek hex means six and we already know that decimal means tenth. Combing the two we get hexadecimal or 16. We still have 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. But we now have 6 additional glyphs to work with for a total of
- For these, the inventors of hexadecimal decided on A - F. The full range of hexadecimal symbols is:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
If you’d like you can go through the same process as earlier, breaking placeholders into columns based on their order of magnitude and doing basic algebra to deserialize, or decode, the decimal value of a hex number. To make things short, programmers love hexadecimal because a byte can be encoded using at most 2 symbols and many times just 1.
1111 1111 (255) in binary becomes FF in hex, and 0000 1010 (ten) is A.
Unicode
We’ve now learned what a counting system is, the differences between decimal, binary, and hexadecimal, as well as how a computer is able to represent different numbers using the only two signals it knows, off or on. But up until now we haven’t touched on memory and how computers store this information that ultimately gets rendered to an application’s UI leading to a possible date with some random person you met on your phone.
ASCII
One of the earliest attempts at character encoding was ASCII, American Standard Code for Information Interchange. ASCII accomplishes two goals:
-
assigns 0 - 127 for a total of 128 numbers to English alphabet letters along with some control commands such as Shift, Backspace.
-
Stores each character in memory as its corresponding value from the chart below.
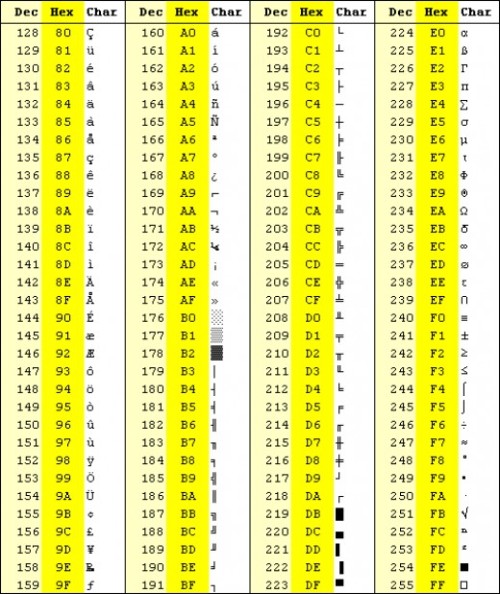
Since 128 values can be stored in 7 bits this means that any ASCII character can be stored in 1 byte (with a whole bit to spare since only 7 of the 8 are used).
Let’s look at an example. Using the chart for reference, lowercase latin a is assigned a value of 97, so a computer encoding text in ASCII will store this character in memory as 01100001 (decimal 97). My name, “Alex” could be stored as:

ASCII works great until you remember that there are over 7 billion people on Earth speaking thousands of languages. Since only 7 bits are required to store every ASCII character people realized there’s one leftover bit to do something with. This extra bit provides 128 more possible characters (2^8). That’s great news, until the Germans decided to use the remaining 128 values to map their own characters, the Russians wanted their own, and the Chinese needed their own as well. You would have a Spanish program that decided 190 meant ñ, while a Chinese program decided that 190 is obviously 波. It would be similar to two persons knowing the same language, English for example, but interpreting the meaning of words in completely different ways. The word happy to Drew means firetruck, while to Willy it means dog. Nonsense. Someone needed to come up with a common language that all computer programs, no matter what language they were trying to store could correctly translate to the right character given some value. This is exactly what Unicode has been solving for the past few decades.
Unicode
Unicode assigns every character in every language in the entire world a number, which we call a code point. A list of these code points can be found on the Unicode website and are represented using “U+n” where U+ says this is a Unicode code point and n is the value represented in hexadecimal. Unicode code points 0 - 127 are 1:1 the same with ASCII values, which we’ll see in a minute can be very useful.
For example Latin capital A is U+41 (decimal 65), a is U+61 (decimal 97), and 💩is U+1F4A9 (decimal 128169)
We’ve gone over how Unicode maps characters to some numerical value and denotes them in hex, but we haven’t talked about how these characters are actually stored in memory. ASCII was able to store every one of its 128 values in 1 byte, but many Unicode values are much larger than 255, like the pile-of-poop emoji seen above. This is because Unicode says nothing about how a value is stored in memory. It simply says I’ll map a character to a number and if you can give me that number, I’ll give you the character. To actually store a character’s value Unicode needs an encoding scheme to translate the number into bytes. To better understand this we’ll look at one of the most common encoding schemes, UTF-8.
UTF-8
Since Unicode just maps characters to values, encoding schemes are used to actually translate these values into bytes. UTF-8 is one of many variable-width encodings. This means that If a Unicode value is less than 255 UTF-8 will store this character in 1 byte, otherwise it will use as many bytes as it needs to store the character. Because of this, characters with Unicode values < 255 encoded with ASCII (represented by 0 -127) or UTF-8 will look the exact same in memory. This means any ASCII encoded document can be read without any problems using UTF-8! Some other encoding schemes you’ve probably heard of are UTF-16, and UTF-32, with UTF-16 using at minimum 2 bytes (16 bits) to store a character and UTF-32 using at minimum 4 bytes, (32 bits), causing them to be incompatible with ASCII. Therefore the most important rule whenever working with text is to ALWAYS KNOW THE ENCODING! Due to the vast number of encodings that all look very similar at the byte level this is near impossible and is why HTTP Requests declare the character set used, HTML has a meta tag to declare a character set, and databases are explicitly configured to use a specific charset or encoding.
Solution
That was a lot to go over, but by now you should have a clear answer to our original question - why 海洋 is represented using 3 bytes and foo only one, assuming these characters were encoded with UTF-8, which Go source code is.
I almost forgot! Lauren is still waiting for a response, and we have a bug to fix! The fix is pretty simple. In Go, as previously stated, strings are just arrays of bytes. We now know that characters are just combinations of bytes. Go provides the Rune type to describe a character as a single unit (regardless of number of bytes) So instead of checking the length of the array of total bytes, we can covert the string to any array of its individual characters, or Runes as Go calls them, and take the length of this array.
fmt.Println([ ]rune("海洋"))
=> [28023, 27915]
fmt.Println(len([] rune("海洋")))
=> 2
Update: Despite the bug-fix, Lauren didn’t find character encodings, or cacti emojis (emoji plural?) as rad as I do, and it never quite worked out. Questions, comments? Reach out on twitter @askwheeler or find me on GitHub!