On Feature Flipping, Deli Coffee, and Hashing Algorithms
Life’s full of goods and bads.
Surfing. Good. Warm beer. Bad
In-N-Out animal style fries. Really good.
Rush hour L train traffic. Really bad.
Modern digital computers might be binary, but the world isn’t. There’s a whole list of things that fall somewhere in the middle. They’re not really good, and not totally bad. They’re good enough.
-
Deli coffee - its no Blue Bottle, but it gets the job done.
-
Dollar slice pizza - It will never approach Prince Street’s level, but at 4am who cares?
-
pseudorandomness - …
Each of the above examples is a worthy candidate for today’s post, but this is a programming blog and you bet we’ll be talking about programming. Let’s look at pseudorandomness and use it to prove why sometimes in software good enough can be, well…good enough.
What would we do without Google? (read: StackOverflow). A quick search and 200ms later Merriam-Webster dictionary is breaking this fancy word down for us:
pseudo - “being apparently rather than actually as stated” synonym: sham
random - “without definite aim, direction, rule, or method”
Pseudorandomness is when something seems like it was generated without any rhyme or reason, when it actually did follow a series of rules. Not truly random, but random enough.
Even if this is the first time you’ve seen this word, it surely isn’t the first time you’ve experienced it. Think about the last time you played music on shuffle. Wasn’t it rad how your computer randomly flipped through songs, avoiding you the pain of having to listen to that playlist in the same order as yesterday’s morning commute. The truth is the song picks weren’t actually random, but that didn’t matter to you, did it? They were chosen pseudorandomly - not truly random, but random enough.
Our computers are great at lots of things. Performing complex calculations, predicting the outcome of events, even mining cryptocurrencies, but if there’s one thing they’re horrible at, its randomness. The problem is your computer is actually really dumb. It not only needs to be told what to do, but also exactly how to do it. This includes generating randomness.
side note: You haven’t experienced how dumb these machines really are until you’ve had a compiler scream at you for forgetting a semicolon.
Luckily computer scientists have been working on this problem of randomness for a long time and they’ve gotten pretty good at it as demonstrated by the shuffle example. The other day, while reviewing a pull request on a popular open source project I collaborate on, I came across a few lines of code that show a great use case for pseudorandomness. I figure if I find them cool then you might too. Let’s walk through this code with the intention that by the end of this post we’ll be equipped with concrete examples as to how us software developers can use pseudorandomness to build software that is good enough.
Flipper is an open source Ruby gem that makes feature flipping easy, while having minimal impact on your application no matter your data store, throughput, or experience. Let’s say our engineering team at VTS just finished a brand new Net Effective Rent (NER) calculator. Before we roll it out to all users we’d like to test it with a subset. This is what Flipper lets us do. We can enable this calculator for:
-
specific user
-
group of users
-
percentage of users
-
percentage of time
-
all actors
Flipper calls each of these ways a feature can be enabled a gate. As for all actors: An actor is anything that responds to flipper_id. For today’s conversation we’ll keep it simple and say an actor is a user, but its good to keep in mind this could be anything.
Flipper definitely lives up to its goal of being easy to use. You create features and enable them for one of these five options. As users access a page with said feature, your code asks Flipper “is this feature enabled for this user?”. Flipper responds true or false.
e.g. enabling a feature for specific users
user = User.find(1)
user2 = User.find(2)
flipper[:ner_calculator].enable(user)
flipper[:ner_calculator].enabled?(user)
=> true
flipper[:ner_calculator].enabled?(user2)
=> false
While I’d love to spend time talking about all of these gates in depth, the README does a great job. Instead, let’s focus on two of the more interesting gates.
-
percentage of time
-
percentage of actors
Percentage of Time
The percentage of time gate allows you to enable a feature for a given percentage of time. A feature that is enabled for 20% of the time means that 20% of the time a user navigates to a page with that feature it will be on. The other 80% it will be off. Put another way if we call
flipper.enabled?(user)
one hundred times it should return true 20 out of the 100 invocations. While there aren’t tons of use cases for this, there are a few. A great use case for the percentage of time gate is load testing. We’d like to see how our application responds to different numbers of users interacting with it. We start with a small percentage, say 5%. This means that 5% of users visiting the page will see the feature. Over the next few weeks we can gradually increase this percentage.
Show me the code!
flipper[:ner_calculator].enabled?(user)
What happens when the above line is evaluated? At the end of the day, or really the end of the call-stack, Flipper invokes a function, open? that returns true if a given user can see a feature, and false otherwise. Every one of the fives gates implements open?.
Can we write an implementation of open? that returns true n% of the time it is
invoked?
def open?(percentage)
end
This is software so of course we can and we’re going to use pseudorandomness to accomplish it. It might not be very obvious at first, but the solution is actually quite simple:
def open?(percentage)
rand < percentage
end
If you’re not familiar with Ruby’s Kernel#rand, no problem, its a core function
that when “called without an argument…returns a pseudo-random floating point
number between 0.0 and 1.0, including 0.0 and excluding 1.0″. Some possible
outcomes of our function given a percentage of 0.5 are:
0.2 < 0.5
0.1 < 0.5
0.6 < 0.5
Assuming rand generates a random enough number we’re expecting that ~50% of the
time the generated number is going to be less than 0.5, which is true.
Just in case you don’t believe me let’s test it out by invoking our function 100 times and counting the number of times it returns true.
(0..100).count { open?(0.5) }
=> 53
Great that looks about right, but to avoid disappointing statistics professors
worldwide (you never know who reads these things), let’s use a more appropriate
sample size. This time we’ll call open?(0.5) a total of 10,000 times, recording
the number of times per 100 calls it returns true.
note: every element in the array is a sample of 100 calls to open?(0.50) and shows the number of times true was returned.
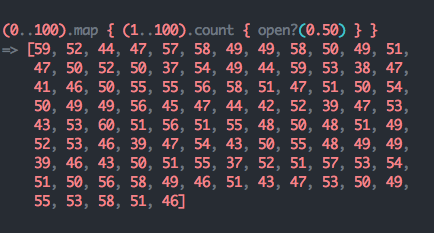
It looks like the majority of the results are ~50, and with a little more code we get a nice visualization using Ruby’s awesome Gruff library.

Let’s also take the average while we’re at it:
(0..100).map { (1..100).count { open?(0.50) } }.reduce(:+) / 100.to_f
On average our open? implementation returns true ~50.44 percent of the time.
It isn’t exactly 50%, but I’d say its damn good enough. You now know how
Flipper’s percentage of time gate implements open?
Hopefully, by now its clear how Flipper is able to turn a feature on for a percentage of time by taking advantage of pseudorandomness to produce a solution that isn’t perfect but undoubtedly works good enough. That leaves us with our next and most interesting question.
Percentage of Actors
How can Flipper turn a feature on for a percentage of users, while consistently returning the same answer when asked whether a given user is enabled without computing and persisting the list of users in some datastore? Taking our current formula, adding another form of pseudorandomness, and topping it off with a bit of creative thinking is all we’ll need to produce a really clever solution.
Given we want to check if a feature is turned on for a user, let’s start with our inputs:
-
User: { id: 1 }
-
Feature: { name: “ner_calculator” }
-
Percentage of time this feature should be on: 30 (note: we’ll use whole number representations of percentages to keep things simple)
If we could get a deterministic pseudo-random number based on the given user and feature then we should be able to use the same approach as above. Something along the lines of:
def open?(user, feature, percentage)
rand(user, feature) < percentage
end
We know we can’t use rand as it only accepts one integer argument, not a user
or feature. This is where Flipper gets very clever. I’ll show a simplified
example (as to avoid needing to understand any of the implementation details
such as how Flipper stores values in your datastore) of how Flipper
accomplishes the percent of actors gate, and then explain step-by-step what’s
going on.
def open?(user, feature, percentage)
id = "#{user.id}#{feature.name}"
Zlibcrc32(id) % 100 < percentage
end
Genius. The interesting idea here is figuring out how to generate a random number given a user and a feature. The key point is that this random number needs to always be the same number given the same inputs. Otherwise this gate would act more like a percentage of time gate and sometimes say yes this feature is enabled for this user and other times say no. Flipper accomplishes this via the crc32 checksum, a commonly used algorithm to detect accidental changes to data sent over a network, as a hashing function. Hashing algorithms take some input and (ideally) produce a unique output. Crc32 serves as a great hashing algorithm for our case because its efficient and only produces integers unlike some other hashing algorithms such as SHA-1 and MD5 that produce alphanumerics. The important thing to note here is that crc32 isn’t a perfect solution for our use case, but its good enough. The outputs aren’t random or else we’d end up with non-deterministic values. They’re just seemingly random!
e.g. crc32 checksum of two similar strings. Notice there is seemingly no similarity between the two produced values despite the similarity of inputs. Given the same inputs the output will always be the same.
Zlib.crc32("alex")
=> 2772900818
Zlib.crc32("Rlex")
=> 1205423261
Zlib.crc32("Rlex")
=> 1205423261
One more hashing function to make sure we all understand the high-level idea because it is important for this conversation. Say we have a hash function that given a string input returns the sum of its bytes.
def hash_str(str)
str.bytes.reduce(:+)
end
Hashing a few strings:
hash_str("ruby")
=> 450
hash_str("Alex")
=> 394
At first this might seem like a decent hash function, but its actually horrible. Without even getting into the issues with passing in strings with varying encodings (Definitely check out my post on character encodings if you’re not up to speed on how computers handle characters. hint: “Alex” might not always sum to 394), its a bad hash function because its capable of producing many collisions. A collision is when two or more inputs hash to the same output. By simply rearranging the characters we’re not changing the total number of bytes so:
hash_str("xlAe")
hash_str("eAlx")
hash_str("lxeA")
all hash to 394! - assuming we’re working with ASCII or UTF-8 encoded strings.
Back to Flipper.
open? takes the user’s id and concatenates it with the feature name.
def open?(user, feature, percentage)
id = "#{user.id}#{feature.name}"
Zlibcrc32(id) % 100 < percentage
end
Substituting id with its value for a user with id: 22 and feature name: :ner_calculator. We get:
Zlib.crc32("22ner_calculator") % 100 < percentage
Futher reducing the lefthand side of the equation we calculate the crc32 checksum of “22ner_calculator” to get:
1316767308 % 100 < percentage
Since crc32 checksums are large integers we mod the result by 100 to get a value between 0 and 100:
8 < percentage
Finally we stated we’re checking this user and feature with a percentage of 30:
8 < 30
At last Flipper tells us, “Yes, Alex, this user is enabled for this feature based on this percentage”:
=> true
Hopefully you’ve learned something and have a new-found appreciation for randomness! Be sure to check out the actual source code as you’re armed with enough knowledge to know exactly how these features are implemented.